Dadansoddiad ystadegol
Dadansoddi a chyflwyno data a gasglwyd
Mae dadansoddi ystadegol yn golygu trin gwahanol fathau o ddata. Gall data fod naill ai’n gategorïaidd neu’n rhifol.
Data categorïaidd
Mae set o ddata yn gategorïaidd os gellir trefnu’r gwerthoedd neu’r arsylwadau sydd yn perthyn iddo yn ôl categori. Mae enghreifftiau o ddata categorïaidd yn cynnwys rhyw, gyda chategorïau ‘gwrywaidd’ a ‘benywaidd’ a grŵp gwaed.
Mae pob gwerth yn cael ei aseinio o set o gategorïau nad ydynt yn gorgyffwrdd. Dylid dewis categorïau yn ofalus oherwydd gall dewis gwael effeithio ar ddeilliant yr ymchwiliad. Mae grŵp oedran yn fath o amrywiolyn categorïaidd sydd yn enghraifft o’r gofal sydd ei angen wrth ddewis amrywiolion categorïaidd. Dylid dewis grwpiau oedran yn ofalus fel na dylanwadir ar y canlyniadau, ac ni ddylent orgyffwrdd, er enghraifft:-
20-29, 30-39, 40-49 Not 20-30, 30-40, 40-50
Gall data categorïaidd fod yn naill ai’n enwol neu’n drefnol
Data enwol
Mae gwerthoedd/arsylwadau data enwol yn gategorïau na roddwyd mewn trefn. Dywedir bod set o ddata yn enwol os gellir aseinio cod ar ffurf rhif pan mai labeli yn unig yw’r rhifau i’r gwerthoedd /arsylwadau sydd yn perthyn iddo. Gallwch gyfrif ond nid trefnu na mesur data enwol. Er enghraifft, mewn set data, gellid codio gwrywod fel o, menywod fel 1, gellid codio grwpiau gwaed fel 0, 1,2,3,4 etc.
Mae’r ffaith eu bod wedi eu codio yn wahanol yn nodi priodoledd yn hytrach nag yn awgrymu gwahaniaeth cymharol yn y data.
Data trefnol
Mae set o ddata yn drefnol os gellir rancio’r (rhoi mewn trefn) gwerthoedd neu’r arsylwadau sydd yn perthyn iddo, neu atodi graddfa. Gallwch gyfrif a threfnu, ond mid mesur data trefnol.
Mae gan gategorïau set drefnol o ddata drefn naturiol, er enghraifft gallai ymatebion i holiadur berthyn i bum categori:-
Anghytuno’n gryf Anghytuno Niwtral Cytuno Cytuno’n gryf
Yn aml rhoddir codau rhifol i amrywiolion trefnol: felly yn yr holiadur enghreifftiol efallai y byddwn yn codio’r ymateb fel rhif rhwng 1 (anghytuno’n gryf) a 5 (cytuno’n gryf). Ond ni allwn ddweud bod ymateb o 4 yn ddwywaith cymaint â 2: mae cyfrifo ymateb cyfartalog yn ddiystyr fel arfer.
Enghraifft arall fyddai dosbarthu yn ôl arferion ysmygu, er enghraifft:-
Erioed wedi ysmygu Cyn-ysmygwyr Ysmygwyr ysgafn Ysmygwyr trwm
Byddai angen i’r categorïau gael eu diffinio’n glir ar y dechrau cyn poblogeiddio cronfa ddata
Data rhifol
Mae data rhifol yn feintiol ac maent yn deillio o fesuriadau neu gyfrifiadau. Gall data rhifol fod yn arwahanol neu’n barhaus.
Data arwahanol
Dywedir bod set o ddata yn arwahanol os mai dim ond gwerthoedd neilltuol ellir eu rhoi i’r arsylwadau sydd yn perthyn iddo, cyfanrifau fel arfer, o fewn ystod penodol. Un enghraifft fyddai nifer y cleifion mewn meddygfa neu nifer y plant mewn teulu. Nid yw’n bosibl cael 673.5 o gleifion ar restr meddygfa.
Data parhaus
Dywedid bod set o ddata yn barhaus os gellir rhoi unrhyw werth o fewn ystod cyfyngedig neu anghyfyngedig i’r gwerthoedd / arsylwadau sydd yn perthyn iddo. Gallwch gyfrif, trefnu a mesur data parhaus. Mae enghreifftiau o ddata parhaus yn cynnwys taldra, pwysau, tymheredd neu odran. Mae’r rhan fwyaf o ddata parhaus yn gyfyngedig oherwydd cywirdeb y mesuriadau y gellir eu gwneud, fel arfer bydd pwysedd gwaed yn cael ei roi i’r mm o Hg agosaf er enghraifft, ond mewn egwyddor gellir rhoi unrhyw werth iddo.
Arddangos data
Histogram
Mae histogram yn arddangos data parhaus mewn colofnau a drefnwyd. Mae’r categorïau yn perthyn i fesuriadau parhaus megis amser, modfeddi, tymheredd etc. Mae’r enghraifft ganlynol (Ffig.2) yn arddangos imiwneiddiadau a roddir yn ystod cyfnod o ddeuddeg mis mewn meddygfa brysur, gan ddisgrifio natur barhaus y data a ddangosir.
Ffigwr 2.
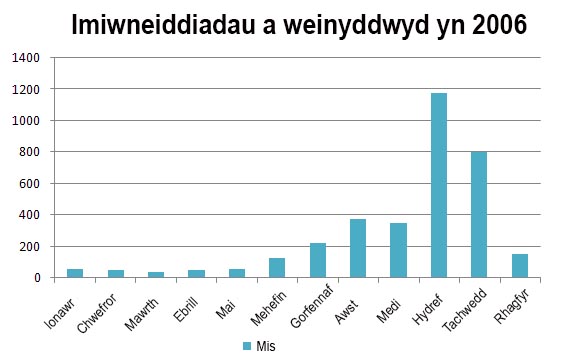
Tabl amledd
Mae tabl amledd yn ffordd o grynhoi set o ddata. Mae’n gofnod o ba mor aml y mae pob gwerth (neu set o werthoedd) sydd yn perthyn i’r amrywiolyn yn digwydd. Gellir dyrchafu hynny drwy ychwanegu canrannau sydd yn perthyn i bob categori. Defnyddir tabl amledd i grynhoi data categorïaidd, enwol a trefnol. Gellir hefyd ei ddefnyddio i grynhoi data parhaus ar ôl rhannu’r set data i grwpiau synhwyrol.
Mae’r enghraifft ganlynol (Tabl 6) yn dangos, ar ffurf tablaidd, amledd diagnosis o angina mewn cleifion a gofrestrwyd mewn practisau mewn nifer o ardaloedd, a’r niferoedd a’r canrannau cyfatebol sydd yn cymryd aspirin.
| Ardal | Cyfanswm Cleifion | % mynychder angina | Nifer y cleifion sydd yn cymryd aspirin | Canran cydymffurfio |
|---|---|---|---|---|
| 1 | 3360 | 1.7 | 2496 | 74 |
| 2 | 1192 | 3.1 | 812 | 68 |
| 3 | 1051 | 2.2 | 765 | 73 |
| 4 | 1011 | 2.3 | 578 | 57 |
| 5 | 930 | 2 | 731 | 79 |
| 6 | 906 | 1.7 | 750 | 83 |
| 8450 | 2 | 6132 | 73 |
Siart gylch
Mae siart gylch yn ffordd o grynhoi set o ddata categorïaidd. Mae’n gylch sydd wedi ei rannu yn segmentau. Mae pob segment yn cynrychioli categori penodol. Mae arwynebedd pob segment yn gymesur i nifer yr achosion yn y categori hwnnw. Mae’r enghraifft ganlynol (ffig.3) yn arddangos ystod a dosbarthiad darlleniadau Hba1C cleifion mewn clinig diabetig. Gall anawsterau godi wrth gymharu dwy set o ddata.
Ffigwr 3
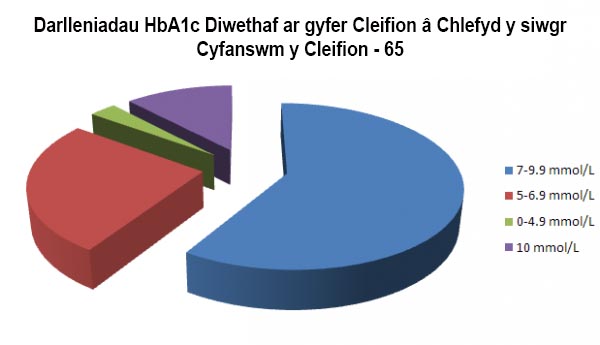
Siart bariau
Mae siart bariau yn ffordd o grynhoi set o ddata categorïaidd. Maent yn cael eu defnyddio’n aml wrth ddadansoddi data archwiliadol er mwyn arddangos prif nodweddion dosbarthiad y data mewn ffordd gyfleus. Mae’n arddangos y data drwy ddefnyddio nifer o betryalau, o’r un lled, a phob un yn cynrychioli categori penodol. Mae hyd (ac arwynebedd) pob petryal yn gymesur i nifer yr achosion yn y categori mae’n ei gynrychioli, er enghraifft, grŵp oedran, crefydd.
Defnyddir siartiau bariau i grynhoi data enwol neu drefnol a gellir eu dangos yn llorweddol neu’n fertigol ac fel arfer maent yn cael eu llunio gyda bwlch rhwng y bariau (petryalau), tra bod y bariau mewn histogram yn cael eu gosod yn sownd i’w gilydd.
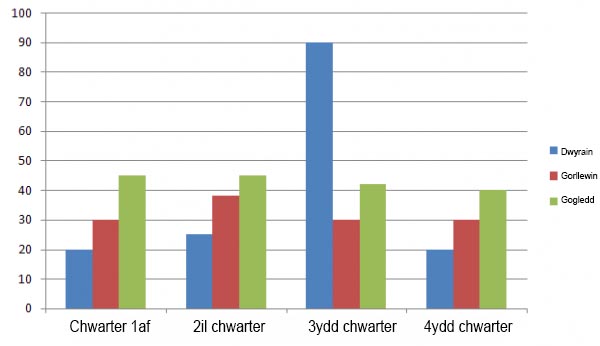
Allanolyn
Allanolyn yw arsylwad mewn set data sydd yn bell o ran gwerth o’r gweddill mewn set data. Mae'n werth anarferol o fawr neu fach o’i gymharu â’r gweddill.
Gall allanolyn fod yn ganlyniad i wall o ran mesur, ac yn yr achos hwnnw bydd yn effeithio ar ddehongli’r data, ac yn effeithio’n amhriodol ar nifer o ystadegau crynodol, er enghraifft y cymedr.
Os yw’r allanolyn yn ganlyniad gwir, mae’n bwysig oherwydd gall fod yn arwydd o ymddygiad eithafol mewn perthynas â’r broses gaiff ei hastudio. Am y rheswm yma mae’n rhaid archwilio pob allanolyn yn ofalus cyn gwneud unrhyw dadansoddi. Ni ddylid dileu allanolion heb gyfiawnhau hynny.
Cymedr y sampl
Cymedr y sampl yw amcangyfrifyn sydd ar gael ar gyfer amcangyfrif cymedr y boblogaeth. Mae’n fesur o leoliad, a elwir yn gyffredin yn gyfartaledd, sydd yn aml yn cael y symbol ẍ
Enghraifft
Pan fo’r set data yn: 5 3 54 93 83 22 17 19. Cyfrifir cymedr y sampl drwy gymryd swm holl werthoedd y data a rhannu hynny gyda chyfanswm nifer y gwerthoedd yn y data:
Mae ei werth yn dibynnu’n union yr un faint ar yr holl ddata, allai gynnwys allanolion. Efallai na fydd yn ymddangos yn gynrychioliadol o ardal ganolog yn achos setiau data sgiw. Mae’n arbennig o ddefnyddiol o ran cynrychioli’r sampl cyfan ar gyfer defnyddio hynny mewn cyfrifiadau dilynol.
Canolrif
Y canolrif yw’r gwerth sydd hanner ffordd drwy set o ddata mewn trefn, a cheir nifer hafal o werthoedd data is ac uwch. Er enghraifft, mae Tabl 7 yn dangos odrif o werthoedd data (21), a’r un canolog yw 48 yn yr achos hwn, gweler isod;
Tabl.7
|
Data |
96 48 27 72 39 70 7 68 99 36 95 4 6 13 34 74 65 42 28 54 69 |
|
Data mewn Trefn |
4 6 7 13 27 28 34 36 39 42 48 54 65 68 69 70 72 74 95 96 99 |
|
Canolrif |
48, gan adael 10 gwerth is a 10 gwerth uwch. |
Pan geir eilrif o werthoedd data, fel yn achos Tabl 8 isod, y canolrif yw’r pwynt rhwng y ddau rif canolog. Yn yr achos yma mae yna 20 o werthoedd data a’r ddau werth canolog yw 47 a 49, felly y canolrif yw’r pwynt sydd yn union rhwng y ddau rif yma h.y. 48.
Tabl.8
|
Data |
57 55 85 24 33 49 94 2 8 51 71 30 91 6 47 50 65 43 41 7 |
|
Data mewn Trefn |
2 6 7 8 24 30 33 41 43 47 49 50 51 55 57 65 71 85 91 94 |
|
Canolrif |
Hanner ffordd rhwng y ddau bwynt data ‘canol’ - yn y achos yma |
|
adio 47 a 49 a rhannu â 2 = 48 |
Yn gyffredinol mae’n fesur disgrifiadol da o’r lleoliad sydd yn gweithio’n dda yn achos data sgiw neu ddata gydag allanolion. Y canolrif yw’r chwartel 0.5.
Modd
Y modd yw’r gwerth sydd yn digwydd amlaf mewn set o ddata arwahanol. Gall fod yna fwy nag un modd os bydd dau werth neu ragor yr un mor gyffredin â’i gilydd. Er enghraifft, cymerer bod canlyniadau arholiad Ystadegau diwedd tymor yn cael eu dosbarthu fel a ganlyn:
Sgôr Myfyrwyr: 1..............94 4………90 7……….90
2..............81 5………70 8……….90
3..............56 6………65 9……….30
Y modd (sgôr mwyaf cyffredin) yw 90, a’r canolrif (sgôr canol) yw 81.
Gwasgariad
Nid yw’r gwerthoedd data mewn sampl i gyd yr un fath. Gelwir y gwahaniaeth yma rhwng gwerthoedd yn wasgariad. Pan fo’r gwasgariad yn fawr, mae’r gwerthoedd wedi eu gwasgaru yn eang; pan fo’n fychan, maent wedi eu clystyru yn agos. Mae lled diagramau megis plotiau dot, plotiau blwch, plotiau bôn a dail yn fwy yn achos samplau sydd â mwy o wasgariad a vice versa. Mae yna nifer o fesuriadau gwasgariad, a’r un mwyaf cyffredin yw gwyriad safonol. Mae’r mesurau yma yn dangos i ba raddau y mae arsylwadau unigol mewn set data wedi eu gwasgaru o gwmpas y cymedr. Yn achos set o fesuriadau, mae cywirdeb uchel yn gysylltiedig â gwasgariad isel.
Ystod
Mae ystod sampl (neu set data) yn fesur o daeniad neu wasgariad yr arsylwadau. Dyma’r gwahaniaeth rhwng gwerth arsylladwy mwyaf a lleiaf rhai nodweddion meintiol, ac mae’n hawdd i’w gyfrifo. Mae llawer o wybodaeth yn cael ei anwybyddu wrth gyfrifo’r ystod oherwydd mai dim ond y gwerthoedd mwyaf a lleiaf a ystyrir; mae gweddill y data yn cael ei anwybyddu. Effeithir yn fawr ar werth ystod set data gan bresenoldeb un gwerth anarferol o fawr neu fach yn y sampl (allanolyn).

